Blogger Ali TtphS: Mudah Memahami Regresi Logit

Dalam salah satu tulisan di blog ini, kita sudah pernah membahas bagaimana memperlakukan variable independent (variable bebas) yang bersifat kualitatif (skala pengukuran nominal atau ordinal) dalam model regresi, yaitu dengan membentuk variable dummy.

Nah, pada tulisan kali ini kita akan melihat bagaimana jika dalam model regresi tersebut yang bersifat kualitatif adalah variable dependent (terikat). Dalam model dengan variabel kualitatif, terdapat beberapa macam teknik pendekatan model yang salah satunya adalah model logit yang menjadi focus dalam tulisan ini. Selain itu, tulisan ini juga lebih menfokuskan pada variable kualitatif yang hanya mempunyai dua kemungkinan nilai, misalnya kesuksesan (sukses – gagal), kesetujuan (setuju – tidak setuju), keinginan membeli (ya – tidak). Variabel kualitatif yang hanya mempunyai dua kemungkinan nilai ini disebut dengan variable biner. (Pada tulisan-tulisan berikutnya, mudah-mudahan akan kita bahas untuk variable kualitatif dengan lebih dari dua kemungkinan nilai).

Selanjutnya, dalam mengestimasi model logit juga terdapat beberapa metode yaitu metode maximum likelihood, noninteractive weighted least square dan discriminant function analysis. Namun demikian, metode yang umum digunakan dalam software paket-paket statistic adalah metode maximum likelihood. Tulisan menggunakan program Minitab yang juga mengaplikasikan metode maximum likelihood dalam estimasi model logit.

Sesuai dengan judul tulisan kali ini, kita tidak akan membahas teori-teori model logit dan maximum likelihood, tetapi lebih pada penekanan bagaimana mengolah data dan menginterpretasikan hasilnya. Bagi yang berminat mendalami teori-teori yang melatarbelakanginya, tersedia banyak literature yang terkait dengan hal tersebut.

Misalnya kita ingin memprediksi bagaimana pengaruh umur, jenis kelamin dan pendapatan terhadap pembelian mobil. Berdasarkan hasil survai terhadap 130 responden, didapatkan datanya sebagai berikut: (silakan download di sini, masih dalam bentuk word, tetapi bisa anda copy ke Minitab).

Dimana:

Y : 1 = jika konsumen membeli mobil; 0 = jika konsumen tidak membeli mobil

X2: umur responden dalam tahun

X3: 1= jika konsumen berjenis kelamin wanita; 0 = jika konsumen berjenis kelamin pria

X4: 0= jika konsumen berpendapatan rendah; 1 = jika konsumen berpendapatan sedang; 2= jika konsumen berpendapatan tinggi

Pengolahan data dilakukan melalui tahapan-tahapan berikut:
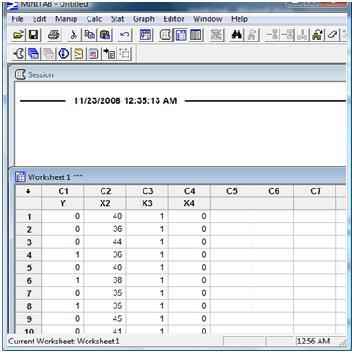
1. Buka program Minitab. Tampilan awal program Minitab terdiri dari dua halaman. Halaman atas dinamakan halaman Session, untuk tampilan perintah dan hasil. Halaman bawah dinamakan halaman worksheet untuk penulisan data.
2. Ketik data di halaman worksheet, atau sebagai latihan copy data seperti yang diberikan di tas. (lihat tampilan 1)

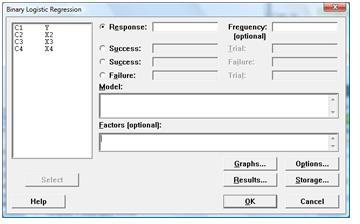
3. Setelah itu klik Stat> Regression> Binary Logistic Regression. Kotak dialog yang ditampilkan sebagai berikut:

4. Isikan pada kotak Response variabel Y dengan cara, klik kotak response, klik variabel Y kemudian klik Select. Selanjutnya isikan pada model variabel X2,X3 dan X4 dengan cara klik kotak Model, klik (atau blok sekaligus) X2, X3 dan X4, kemudian klik Select.

Selanjutnya, karena variabel X4 merupakan peubah kategori (ordinal) dengan lebih dari kategori (yaitu 0=pendapatan rendah, 1=pendapatan sedang dan 2=pendapatan tinggi) maka diubah terlebih dahulu ke dalam 2 variabel dummy, untuk mengembangkan model yang logis dan mudah diinterpretasi, sebagai berikut:

X4_1 = 1, jika konsumen berpendapatan sedang; 0 = jika selainnya

X4_2 = 1, jika konsumen berpendapatan tinggi; 0 = jika selainnya

Dalam program Minitab untuk mengkonversi ini dengan cara memasukkan peubah X4 ke dalam kotak isian Factors. Dengan cara demikian, Minitab secara otomatis akan menjadikan variabel X4 menjadi dua variabel dummy yaitu X4_1 dan X4_2. Peubah X3 sebenarnya juga dapat dimasukkan ke dalam kotak isian Factors, tetapi karena berisi data numerik ( 1 atau 0) maka tidak perlu dimasukkan.

Hasil pemasukan variabel tersebut dapat dilihat dalam tampilan berikut:

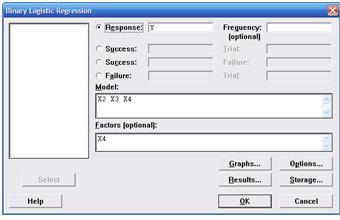
5. Setelah itu klik, OK. Maka akan muncul hasil regresi logit di halaman Session sebagai berikut (disini hanya ditampilkan bagian-bagian terpenting saja yang akan dibahas):

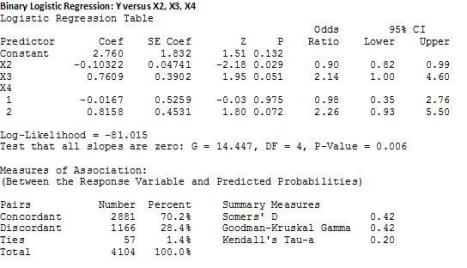
Dalam pelaporannya, model regresi logistiknya dapat dituliskan sebagai berikut:

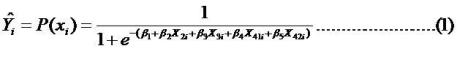
Yang dari output minitab contoh kita menjadi sebagai berikut:

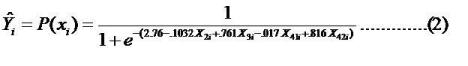
Model ini merupakan model peluang membeli mobil [(P(x_i)] yang dipengaruhi oleh faktor-faktor umur, jenis kelamin dan pendapatan. Dapat kita lihat bahwa model tersebut adalah bersifat non-linear dalam parameter. Selanjutnya, untuk menjadikan model tersebut linear, maka dilakukan transformasi dengan logaritma natural, (transformasi ini yang menjadi hal penting dalam regresi logistik dan dikenal dengan istilah “logit transformation”), sehingga menjadi:

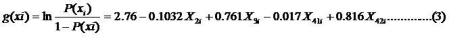
1-P(x_i) adalah peluang tidak membeli mobil, sebagai kebalikan dari P(x_i) sebagai peluang membeli mobil. Oleh karenanya, ln [P(x_i)/1-P(x_i)] secara sederhana merupakan log dari perbandingan antara peluang membeli mobil dengan peluang tidak membeli mobil. Oleh karenanya juga, koefisien dalam persamaan (3) ini menunjukkan pengaruh dari umur, jenis kelamin dan pendapatan terhadap peluang relative individu membeli mobil yang dibandingkan dengan peluang tidak membeli mobil.

Sebagaimana halnya dengan model regresi linear dengan metode OLS, kita juga dapat melakukan pengujian arti penting model secara keseluruhan. Jika pada metode OLS kita menggunakan uji F, maka pada model ini, kita menggunakan uji G. Statistik G ini menyebar menurut sebaran Khi-kuadrat (χ²). Karenanya dalam pengujiannya, nilai G dapat dibandingkan dengan nilai χ² tabel pada α tertentu dan derajat bebas k-1. (kriteria pengujian dan cara pengujian persis sama dengan uji F pada metode regresi OLS). Tetapi, anda juga bisa melihat nilai p-value dari nilai G ini yang biasanya ditampilkan oleh sofware-software statistik.

Dari hasil Minitab kita, didapatkan nilai G sebesar 14,447 dengan p-value 0,006. Karena nilai ini jauh dibawah 10 % (jika kita menggunakan pengujian dengan α=10%), atau jauh dibawah 5% (jika kita menggunakan pengujian dengan α=5%), maka dapat disimpulkan bahwa model regresi logistik secara keseluruhan dapat menjelaskan atau memprediksi keputusan konsumen dalam membeli mobil.

Selanjutnya, untuk menguji faktor mana yang berpengaruh nyata terhadap keputusan pilihan membeli mobil tersebut, dapat menggunakan uji signifikansi dari parameter koefisien secara parsial dengan statistik uji Wald, yang serupa dengan statistik uji t atau uji Z dalam regresi linear biasa, yaitu dengan membagi koefisien terhadap standar error masing-masing koefisien.

Dari output minitab ditampilkan nilai Z dan p-valuenya. Dari hasil kita, berdasarkan nilai p-value (dan menggunakan kriteria pengujian α=10%), kita dapat melihat seluruh variabel (kecuali X4_1), berpengaruh nyata (memiliki p-value dibawah 10%) terhadap keputusan membeli mobil.

Lalu, bagaimana kita menginterpretasikan koefisien regresi logit dari persamaan (3) di atas ? Dalam model regresi linear, koefisien β₁ menunjukkan perubahan nilai variabel dependent sebagai akibat perubahan satu satuan variabel independent. Hal yang sama sebenarnya juga berlaku dalam model regresi logit, tetapi secara matematis sulit diinterpretasikan.

Koefisien dalam model logit menunjukkan perubahan dalam logit sebagai akibat perubahan satu satuan variabel independent. Interpretasi yang tepat untuk koefisien ini tentunya tergantung pada kemampuan menempatkan arti dari perbedaan antara dua logit. Oleh karenanya, dalam model logit, dikembangkan pengukuran yang dikenal dengan nama odds ratio (ψ). Odds ratio untuk masing-masing variabel ditampilkan oleh Minitab sebagaimana yang terlihat di atas.

Apa yang dimaksud dengan odds ratio dan bagaimana memahaminya? Odds ratio secara sederhana dapat dirumuskan: ψ = e^β, dimana e adalah bilangan 2,71828 dan β adalah koefisien masing-masing variabel. Sebagai contoh, odds ratio untuk variabel X₃ = e^0.7609 = 2,14 (lihat output minitab).

Dalam kasus variabel X₃ (jenis kelamin dimana 1 = wanita dan 0 = pria), dengan odds ratio sebesar 2,14 dapat diartikan bahwa peluang wanita untuk membeli mobil adalah 2,14 kali dibandingkan pria, jika umur dan pendapatan mereka sama. Artinya wanita memiliki peluang lebih tinggi dalam membeli mobil dibandingkan pria.

Dalam kasus variabel X₂ (umur), dengan odds ratio sebesar 0,90 dapat diartikan bahwa konsumen yang berumur lebih tua satu tahun peluang membeli mobilnya adalah 0,90 kali dibandingkan konsumen umur yang lebih muda (satu tahun), jika pendapatan dan jenis kelamin mereka sama. Artinya orang yang lebih tua memiliki peluang yang lebih rendah dalam membeli mobil.

Dalam konteks umur ini (yang merupakan variabel dengan skala ratio), hati-hati menginterpretasikan nilai perbedaan peluangnya. Jika perbedaan umur lebih dari 1 tahun, misalnya 10 tahun, maka odds rationya akan menjadi 0,36, yang diperoleh dari perhitungan sbb: ψ=e^{(10 x -0.10322)} . Artinya peluang membeli mobil konsumen yang berumur lebih tua 10 tahun adalah 0,36 dibandingkan konsumen yang lebih muda (10 tahun) darinya.

Selanjutnya, dalam konteks variabel pendapatan, terlihat bahwa X₄₁ tidak berpengaruh signifikan. Artinya, peluang membeli mobil antara konsumen pendapatan sedang dan pendapatan rendah adalah sama saja. Sebaliknya, untuk X₄₂, dapat diinterpretasikan bahwa peluang membeli mobil konsumen pendapatan tinggi adalah 2,26 kali dibandingkan pendapatan rendah, jika umur dan jenis kelaminnya sama. (Perhatikan, baik untuk X₄₁ maupun untuk X₄₂, perbandingannya adalah dengan pendapatan rendah. Lihat penjelasan ini lebih lanjut pada tulisan mengenai variabel dummy yang ada di blog ini).

Output Minitab juga menampilkan ukuran-ukuran asosiasi (hubungan) antara nilai aktual (sebenarnya) dari variabel dependent (Y) dengan dugaan peluangnya, yang dapat kita interpretasikan sebagai berikut:

Dari nilai Concordant dapat disimpulkan bahwa 70,2 persen pengamatan dengan kategori membeli (Y=1) diduga mempunyai peluang lebih besar pada kategori membeli. Dari nilai Discordant dapat disimpulkan bahwa 28,4 persen pengamatan dengan kategori tidak membeli (Y=0) diduga mempunyai peluang lebih besar pada kategori membeli. Nilai Ties merupakan persentase pengamatan dengan peluang pada kategori membeli sama dengan peluang kategori tidak membeli. Hubungan yang kuat (dan sekaligus menunjukkan semakin baiknya daya prediksi model) ditandai oleh besarnya nilai Concordant dan kecilnya nilai Discordant dan Ties.

Selanjutnya juga terdapat ukuran-ukuran ringkas (Sommer’s D, Goodman-Kruskal Gamma dan Kendall’s Tau-a). Semakin besar ukuran asosiasi ini ke nilai 1, maka semakin baik daya prediksi dari model dugaan yang diperoleh.